Research Interests

Gender and physics
The small proportion of female students and researchers in physics and
computer sciences is a serious problem for a modern egalitarian society.
This problem can be cured, as shown by the Carnegie Mellon School of
Computer Science, where the proportion of female students went from 7%
to 50%.
After being a gender equality officer at the faculty of science and
engineering of Sorbonne University, I am now collaborating with
two sociologists (Beate Collet and Elise Verley)
and a PhD student (Jeanne Goulpier) to analyze the situation at Sorbonne
University and set up solutions.
Geometric methods in solid-state physics
The tools of differential geometry proved very powerful to solve some
long-standing problems, such as the correct definition of electric and
orbital polarization or the understanding of the quantum Hall effect.
They allowed us to prove that exponentially localized Wannier functions
can be constructed. They also play a prominent role in the discovery of
new phenomena, such as Chern insulators. These concepts, which are new
in solid-state physics but venerable in mathematics, go by the name of
Berry phase, Berry connection, connection on fibre bundles, triviality of
bundles, Chern numbers and de Rham theorem. This is an
exciting field where the unifying picture offered by differential
geometry is very precious.
Quantum fields and quantum groups
Many-body theory and quantum field theory express physical
properties
as infinite sums of Feynman diagrams. These diagrams give a clear
picture
of the physical phenomena but they have poor algebraic properties. It
turns
out that quantum groups provide a powerful algebraic tool for quantum
field
calculations. Wick's theorem is the twisted product of quantum groups,
the expectation value over the vacuum is the counit, quantum states are
positive 1-cochains, etc. In fact the quantum group language is a
natural
framework for bosons and fermion fields, normal products, operator and
time-ordered products, renormalisation. Moreover, the quantum group
concepts
are still valid beyond the usual quantum field framework. For instance,
it is possible to consider noncommutative normal products and
time-ordered
products. Quantum groups can provide an efficient framework to
calculate
the Green functions of degenerate systems.
Quantum fields in curved spacetimes
Quantum fields in curved spacetimes have made tremendous progress through the
efforts of Brunetti, Fredenhagen, Hollands, Wald, Dutsch, Rejzner and coll.
culminating with a background independent formulation of the quantum field theory
of gravitation. Some of these works make heavy use of locally convex topological
vector spaces and convex bornological spaces. There are many excellent textbooks
on locally convex spaces but the results of bornology theory are often
quit difficult to locate. I have scanned some of these texts:
 Bornological library Bornological library |
The colour of minerals
Colour is one of the most obvious properties of minerals and gemstones
but the origin of colour is often quite difficult to determine. For
instance,
it is only recently that we know why fossil ivory of mastodons (13
million
years old) turns blue when heated, so blue that it was used as a
substitute
for turquoise in the Middle Age. The colour of ruby and emerald is due
to the presence of chromium impurities surrounded by a distorted
octahedron
of oxygen. But the reason why ruby is red and emerald is green is not
clear.
Two theoretical models are used to calculated the colour of minerals
and
gems, (i) Green function and (ii) effective Hamiltonian:
(i) Recently, the colour of semiconductors was calculated successfully
using Green function methods such as the GW approximation and the
Bethe-Salpeter
equation. These methods assume that the initial state (before
interaction)
is degenerate.
(ii) The colour of transition metals and rare-earth compounds cannot
be calculated ab initio but the position of the bands in optical
absorption
spectra can be computed by diagonalizing an effective Hamiltonian
depending
on parameters. In this method, the initial state is degenerate but the
values of the parameters must be fitted.
To unify both approaches, we have to set up a Green function method
using degenerate initial states.
Light and biological cells
Light and biological cells have a number of fascinating interactions.
Many animals, mushrooms and bacteria are bioluminescent.
Photosynthesis is also an obvious and vital case of interaction
between light and plant cells.
Only a few species are bioluminescent. However, all living organisms
spontaneously emit a very weak light know as "autoluminescence"
or "ultraweak photon emission" (UPE). This light is in the visible
range and is not due to black body radiation. Autoluminescence
is due to the fact that among the many biochemical reactions
that take place in the cell, some of them are chemiluminescent
(they create excited species that relax radiatively to their ground
states). The most prominent luminescent excited species are thought
to be singlet oxygen and triplet carbonyl.

Pelargonium leaf (K. Creath, A look at some systemic properties
of self-bioluminescence. In The Nature of Light: Light in Nature II,
SPIE Proceedings 7057 (2008) 705708)

Autoluminescence of a human hand (A. Rastogi and P. Pospisil,
Spontaneous ultraweak
photon emission imaging of oxidative metabolic processes
in human skin: effect of molecular oxygen
and antioxidant defense system, J. Biomed. Opt., 16 (2011)
096005)
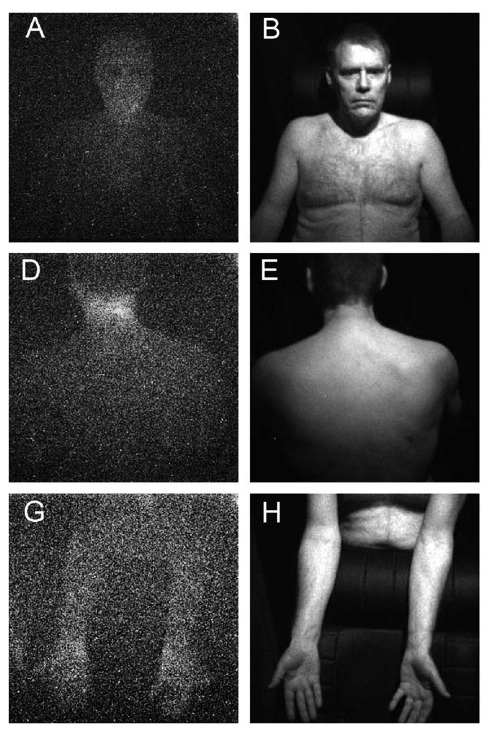
Autoluminescence of a human torso (R. van Wijk, M. Kobayashi
and E. P. A. van Wijk, Anatomic characterization of
human ultra-weak photon emission with a moveable photomultiplier
and CCD imaging, J. Photochem. Photobiol. B, 83 (2006) 69-76
Time-reversal symmetry, parity and x-ray
absorption
The absorption of x-rays by matter is mainly due to electric dipole
transitions
but electric quadrupole transitions can also be observed. Pure electric
dipole and quadrupole transitions are even under parity, in other
words,
they do not distinguish between two samples that are related by an
inversion.
José Goulon realized that the interference between electric
dipole
and quadrupole transitions provides a parity-odd transition operator,
with
which properties of chiral materials can be investigated. On the other
hand, time-reversal symmetry divides the materials into two classes,
those
that are symmetric and those that are not symmetric. The charge is a
time-reversal
symmetric but the spin and the current are reversed by time-reversal.
Thus
time-reversal odd spectroscopies enable us to measure properties of the
electronic current and spin in materials. By using the possible
combinations
of time-reversal, parity and rotation symmetries, three new x-ray
spectroscopies
were discovered: natural circular dichroism (parity odd, time-reversal
even, rank 2), magnetochiral dichroism (parity odd, time-reversal odd,
rank 1) and nonreciprocal linear dichroism (time-reversal odd, rank 2
and
3). As a possible application, these new spectroscopies give unique
information
on the magnetic symmetry group of chiral and magnetoelectric materials.
Rainbows
Drawing a realistic rainbow is not so easy. Two great
rainbow
drawers are Raymond
Lee and Philip
Laven. We developed a theory describing the
scattering
of a partially coherent beam of light by a dielectric sphere. When this
theory is applied to the scattering of sunlight by a raindrop, we
obtain
the following rainbow slices: for raindrop size of 0.1 to 0.5 mm
pdf , for raindrop size of 0.6 to 1
mm
pdf . If the sun were a coherent source
of
light the rainbows would look like this: for raindrop
size
of 0.1 to 0.5 mm pdf,
for raindrop size of 0.6 to 1 mm pdf.
References: R.L. Lee, Mie theory, Airy theory, and the natural
rainbow,
Appl. Opt. 37 (1998) 1506-19; P. Laven, Simulation of
rainbows,
coronas, and glories by use of Mie theory, Appl. Opt. 42
(2003)
436-444; D. Cabaret, S. Rossano, Ch. Brouder, Mie scattering of a
partially
coherent beam, Opt. Commun. 150 (1998) p.239-50.


 Bornological library
Bornological library 

